
Résumé
Après une étude géométrique des ellipses et de leurs propriétés, ce document va particulièrement s’intéresser au mouvement du centre d’un astre vérifiant les lois de Kepler.
Des différentes définitions de l’ellipse, nous allons d’abord donner la plus simple, celle parfois utilisée par les jardiniers pour tracer le pourtour d’un parterre elliptique. Vous pouvez d’ailleurs faire la manipulation vous-même : il suffit de disposer d’une feuille de papier fixée sur une planche en bois, de deux épingles ou punaises, d’un peu de fil à coudre et d’un crayon de faible diamètre. Nous donnerons ensuite une autre méthode de construction de l’ellipse, un peu moins simple mais plus utilisée en astronomie.
Dans un premier temps, attachez les deux extrémités de votre fil à une épingle que vous plantez, matérialisant ainsi un point fixe noté O. Placez votre crayon dans la boucle que forme le fil et tournez autour du point O en maintenant le fil constamment tendu. Vous obtenez ainsi un cercle de centre O et de rayon de valeur a (figure de gauche). Maintenant, enlevez l’épingle du point O et placez deux épingles de part et d’autre du point O, à la même distance c du point O en choisissant c strictement inférieur à a. En conservant au fil la même longueur que précédemment, attachez une extrémité à la première épingle et l’autre extrémité à la seconde épingle. Comme précédemment, placez votre crayon dans la boucle que forme le fil et tournez autour du point O en maintenant le fil constamment tendu. Vous obtenez une ellipse (figure de droite). Les points fixes matérialisés par les épingles (F1 et F2 sur la figures) sont les foyers de l’ellipse. Soit d1 la distance de la pointe M du crayon à F1 et d2 la distance de M à F2. Nous avons évidemment, quelle que soit la position de M sur l’ellipse :
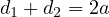 |
(1) |
D’où une définition précise d’une ellipse : soient deux points fixes de l’espace appelés foyers et un plan fixe contenant ces deux points ; l’ellipse est l’ensemble des points de ce plan dont la somme des distances aux deux foyers est une constante.
La distance de F1 à F2 (égale à 2.c) est nécessairement inférieure à la longueur du fil (égale à 2.a). Il faut donc choisir c strictement inférieur à a.
Le rapport (c/a) est appelé excentricité de l’ellipse, on le note habituellement e :
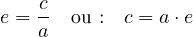 |
(2) |
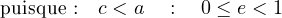 |
(3) |
Remarque : Le cas particulier : c = 0 revient à imaginer les foyers confondus avec le point O : on retrouve le cas particulier du cercle de rayon a. Ainsi, plus l’excentricité est proche de zéro, plus l’ellipse « ressemble » à un cercle, plus l’excentricité augmente, plus l’ellipse « s’aplatit ». À titre d’exemple revenons aux mouvements des centres des planètes décrits dans le référentiel héliocentrique. L’excentricité de l’orbite terrestre est e = 0,0167 ; cette valeur est très faible ; l’orbite est « presque » circulaire comme le montre le schéma n° 3 du document principal. L’excentricité de l’orbite de mars est 5,6 fois plus élevée, quoiqu’encore assez faible : e = 0,0933 ; on voit tout de même sur la figure 3 que la distance soleil – mars varie...
Encore quelques définitions :
* La droite passant par les points A et B et par les foyers de l’ellipse constitue le grand axe de l’ellipse. La distance de A à B vaut 2.a ; a constitue la longueur du demi-grand axe de l’ellipse.
* La droite passant par les points D et O constitue le petit axe de l’ellipse. La distance de O à D, notée habituellement « b », constitue la longueur du demi-petit axe de l’ellipse. Dans le cas particulier où M est en D, nous avons : d1 = d2 = a. Le théorème de Pythagore appliqué au triangle (ODF1) conduit à :
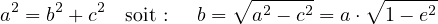 |
(4) |
On commence par tracer un cercle de centre O (centre de
l’ellipse) et de rayon a (longueur du demi grand axe de l’ellipse). La
position
d’un point quelconque Mc
sur ce cercle est repérée par l’angle polaire E, angle entre l’axe (O,x)
et le vecteur position  . Les
coordonnées cartésiennes du point Mc
sont ainsi :
. Les
coordonnées cartésiennes du point Mc
sont ainsi :
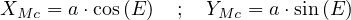 |
(5) |
Pour obtenir l’ellipse d’excentricité e et de demi grand
a, on fait correspondre à tout point Mc
du cercle un point M de l’ellipse
ayant même abscisse que Mc
mais une ordonnée multipliée par le rapport (b/a) (rapport égal à 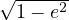 comme démontré au dessus).
Les coordonnées cartésiennes du point M sont ainsi :
comme démontré au dessus).
Les coordonnées cartésiennes du point M sont ainsi :
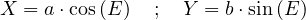 |
(6) |
Pour obtenir l’équation cartésienne de l’ellipse, il suffit de remarquer :
sin2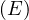 + cos2 + cos2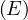 = 1∀E = 1∀E
|
ce qui conduit à :
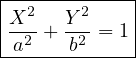 |
(7) |
On peut vérifier que cette méthode est bien cohérente avec la définition de l’ellipse donnée initialement. Sachant que les foyers sont à la distance c = e.a du centre O, le théorème de Pythagore appliqué aux triangles rectangles (F1HM) et (F2HM) conduit à :
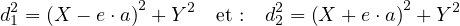 |
(8) |
La première égalité conduit à :
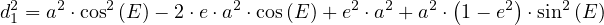 |
(9) |
En tenant compte de la relation déjà évoquée : sin2 + cos2
+ cos2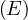 = 1∀E :
= 1∀E :
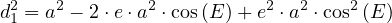 |
(10) |
On reconnaît l’expression générale du carré d’une différence :
![2 2
d1 = [a - e⋅a⋅cos(E )] donc : d1 = a ⋅[1- e ⋅cos(E )]](annexe_1_Trajectoire_elliptique16x.png) |
(11) |
Le calcul pour d2 se mène de la même façon : il suffit de remplacer e par son opposé. Au final nous obtenons :
![d1 = a⋅[1- e⋅cos(E )] et : d2 = a ⋅[1+ e ⋅cos(E )]](annexe_1_Trajectoire_elliptique17x.png) |
(12) |
Cela donne bien, quelle que soit la valeur de l’angle (E), donc quelle que soit la position du point M sur sa trajectoire elliptique :
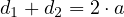 |
(13) |
Nous retrouvons bien la relation de définition initiale de l’ellipse !
On peut choisir l’origine du repère d’étude au foyer F1de
l’ellipse. Pour connaître la position du point M à un instant donné, il
faut
connaître les caractéristiques du vecteur position 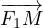 . Ce vecteur peut être défini par deux grandeurs : * la
norme du vecteur, soit la distance de F1à
M, notée jusqu’ici « d1
», souvent aussi notée « r » ;
. Ce vecteur peut être défini par deux grandeurs : * la
norme du vecteur, soit la distance de F1à
M, notée jusqu’ici « d1
», souvent aussi notée « r » ;
* l’angle polaire ν entre
l’axe (O,x) et le vecteur position 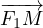 (voir figure n° 2).
L’équation polaire de la trajectoire est l’équation : r
= f
(voir figure n° 2).
L’équation polaire de la trajectoire est l’équation : r
= f . Nous avons déjà démontré la
relation entre r et
E :
. Nous avons déjà démontré la
relation entre r et
E :
![r = d = a⋅[1- e⋅cos(E)]
1](annexe_1_Trajectoire_elliptique22x.png) |
(14) |
Il nous faut donc une relation entre E et ν . Pour cela, il suffit d’appliquer les formules classiques de trigonométrie au triangle rectangle (F1HM) :
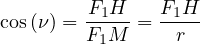 |
(15) |
![F1H = OH - OF1 = a⋅cos(E) - a ⋅e = a ⋅[cos(E)- e]](annexe_1_Trajectoire_elliptique24x.png) |
(16) |
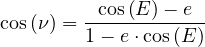 |
(17) |
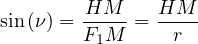 |
(18) |
En exprimant cos(E) dans le triangle (OMcH) puis en tenant compte de la méthode décrite précédemment pour passer du cercle à l’ellipse :
 |
(19) |
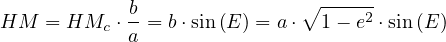 |
(20) |
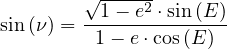 |
(21) |
Sachant que : 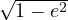 > 0
et
> 0
et ![[1- e⋅cos(E)]](annexe_1_Trajectoire_elliptique31x.png) > 0,
on peut remarquer que sin(E) et sin(ν) sont
nécessairement de même signe. Des
relation (17) et (21), on tire :
> 0,
on peut remarquer que sin(E) et sin(ν) sont
nécessairement de même signe. Des
relation (17) et (21), on tire :
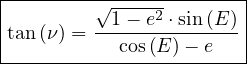 |
(22) |
Remarque : la connaissance de la tangente ne détermine la valeur de l’angle qu’à 180° près. Pour lever l’indétermination, on utilise le fait que sin(E) et sin(ν) sont nécessairement de même signe. Dans les cas très fréquents où l’excentricité est faible devant « 1 », on peut de façon plus simple lever cette indétermination en remarquant que les valeurs de E et ν sont nécessairement très proches.
Autre remarque : on trouve souvent dans la littérature,
la relation (22) remplacée par une relation entre les tangentes des angles
moitiés. Cette nouvelle relation à l’avantage de ne pas introduire
d’ambiguïté sur la connaissance de ν. En
effet, connaître tan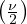 ,
détermine
,
détermine  à 180° près,
donc n’introduit pas d’ambiguïté sur l’anomalie vraie de toutes façon
définie modulo 360°. Pour obtenir
cette relation, on passe aux angles moitié dans la relation (17) :
à 180° près,
donc n’introduit pas d’ambiguïté sur l’anomalie vraie de toutes façon
définie modulo 360°. Pour obtenir
cette relation, on passe aux angles moitié dans la relation (17) :
![-cos(E-)--e-- 2(ν-) 2(ν-) (1-+-e)[1-- cos(E-)]-
cos(ν) = 1- e⋅cos(E) = 1- 2sin 2 ; sin 2 = 2[1- e.cos(E)]](annexe_1_Trajectoire_elliptique35x.png) |
(23) |
![-cos(E-)--e-- 2(ν) 2( ν) (1---e)[1-+-cos(E-)]-
cos(ν) = 1- e⋅cos(E) = 2cos 2 - 1 ; cos 2 = 2[1- e.cos(E)]](annexe_1_Trajectoire_elliptique36x.png) |
(24) |
Division « membre à membre » de ces deux dernières relations :
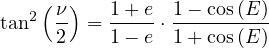 |
(25) |
Même méthode de passage à l’angle moitié qu’aux lignes (23) et (24) :
1 - cos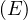 = 2sin2 = 2sin2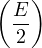 ; 1 + cos ; 1 + cos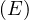 = 2cos2 = 2cos2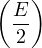
|
Donc :
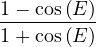 = tan2 = tan2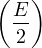
|
En reportant dans l’expression (25), cela donne :
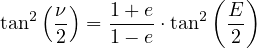 |
(26) |
Les deux tangentes étant toujours de même signe pour ce type de mouvement :
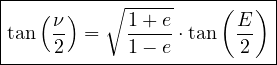 |
(27) |
Nous pouvons maintenant déterminer l’équation polaire de l’ellipse.
Les relations (15) et (16) conduisent à :
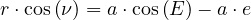 |
(28) |
en remplaçant cos(E) par son expression déduite de la relation (14) :
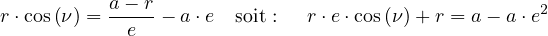 |
(29) |
r = 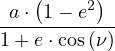
|
On pose souvent : p = a⋅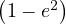 ; p est appelé « paramètre de l’ellipse ».
D’où l’expression « classique » de l’équation polaire de
l’ellipse :
; p est appelé « paramètre de l’ellipse ».
D’où l’expression « classique » de l’équation polaire de
l’ellipse :
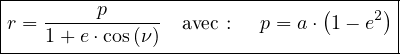 |
(30) |
Remarque : Nous avons
arbitrairement choisi l’origine au foyer F1. Ainsi le cas
particulier E =
ν = 0 correspond à une
distance
minimale de M à F1,
le point M étant en P. Il aurait été possible de choisir
l’origine au foyer F2, en posant : r = F2M, l’angle
polaire ν devenant l’angle entre l’axe (O,x) et le vecteur  . Dans ces conditions, le cas
particulier E =
ν = 0 correspond à une
distance maximale de M à
F2. Des calculs analogues aux précédents conduisent dans ces conditions à
l’équation polaire
suivante :
. Dans ces conditions, le cas
particulier E =
ν = 0 correspond à une
distance maximale de M à
F2. Des calculs analogues aux précédents conduisent dans ces conditions à
l’équation polaire
suivante :
 |
(31) |
Imaginons le disque de rayon a, d’aire π ⋅a2 que l’on cherche à tapisser de carrés identiques. La surface ainsi recouverte est plus petite bien sûr que le disque (voir figure n° 3). Imaginons maintenant que l’on choisisse des carrés dont la longueur de chaque côté est extrêmement petite devant le rayon a du disque : la surface « perdue » (colorée en bleu sur le schéma) devient négligeable : l’aire du disque est égale à la somme des aires des petits carrés : π ⋅a2 = N ⋅l2 où N est le nombre de carrés et l la longueur d’un côté de carreau.
Supposons maintenant que l’on transforme chaque petit
carré de la façon suivante : sa longueur l est conservée mais sa
hauteur est multipliée par le rapport b/a défini précédemment pour
l’ellipse. Conserver les dimensions horizontales en
multipliant les dimensions verticales par le rapport b/a est la méthode
utilisée pour transformer le cercle de rayon « a » en
ellipse : Nos N rectangles tapissent maintenant l’ellipse !
Nous avons un nombre de rectangles égal au nombre
de carrés précédents : N =
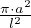 mais l’aire de chaque rectangle est l
⋅
mais l’aire de chaque rectangle est l
⋅ . L’aire totale de ces N rectangles est
donc :
. L’aire totale de ces N rectangles est
donc :
N ⋅ l2 ⋅ = = 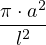 ⋅ l2 ⋅ ⋅ l2 ⋅ = π
⋅ a ⋅ b = π
⋅ a ⋅ b
|
Cette aire est celle de la surface délimitée par l’ellipse. Conclusion : l’aire de la surface délimitée par une ellipse est :
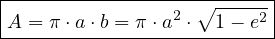 |
(32) |
Attention ! par la suite, la mesure des angles sera exprimée en radians.
Pour l’instant, nous nous sommes limités à une étude purement géométrique de l’ellipse. Nous introduisons maintenant de la dynamique : nous supposons que le centre d’inertie S d’un satellite naturel ou artificiel d’un astre attracteur de centre F décrit, dans un repère galiléen d’origine F un mouvement elliptique. L’étude dynamique rigoureuse du mouvement est largement disponible sur le net, ici par exemple :
Sans refaire ici la démonstration du document cité ci-dessus, nous admettons que S vérifie la loi des aires : soit t = 0 la date de passage de S au périastre ; l’aire de la surface balayée par le segment (FS) entre les dates zéro et t (date quelconque) est, selon la loi des aires, proportionnelle à t.
De plus, dans le cas particulier t = T : période du
mouvement, l’aire de la surface balayée vaut π.a.b
. L’aire de la surface
balayée entre les date zéro et t peut donc s’écrire : A
= 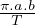 ⋅ t
. On appelle vitesse aréolaire de S le nombre dérivé de A par
rapport à t : vA
=
⋅ t
. On appelle vitesse aréolaire de S le nombre dérivé de A par
rapport à t : vA
= 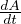 ; soit ici :
; soit ici :
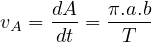 |
(33) |
La loi des aires peut aussi s’énoncer simplement en disant que, lorsqu’elle est vérifiée, la vitesse aréolaire du point S décrivant l’ellipse ne varie pas au cours du temps.
Remarque : dans le cas général d’un astre attracteur quelconque, la position de S la plus proche de F est appelée « périastre » et la position la plus éloignée « apoastre ». Si l’astre attracteur est la terre, ces deux mots peuvent être remplacés respectivement par « périgée » et « apogée ». Si l’astre attracteur est le soleil, ces deux mots peuvent être remplacés respectivement par « périhélie » et « aphélie ».
Exprimons maintenant la vitesse aréolaire en fonction des
coordonnées polaires de M et de leurs dérivées par rapport au temps.
Soit 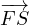 = r
⋅
= r
⋅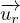 le vecteur position de S à la date quelconque t,
le vecteur position de S à la date quelconque t,  étant un vecteur unitaire. Entre les date t et (t +
dt), le point M
subit un déplacement élémentaire :
étant un vecteur unitaire. Entre les date t et (t +
dt), le point M
subit un déplacement élémentaire : 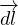 = dr
⋅
= dr
⋅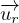 + r
⋅ dν ⋅
+ r
⋅ dν ⋅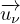 où
où 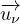 désigne un vecteur unitaire
perpendiculaire à
désigne un vecteur unitaire
perpendiculaire à 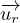 dans le plan de l’ellipse et orienté dans le sens du vecteur déplacement
de S (voir figure n°4). L’aire de la
surface
balayée par le segment (FS) est celle du triangle hachuré sur la figure.
Cette valeur est la demie norme du
produit
vectoriel :
dans le plan de l’ellipse et orienté dans le sens du vecteur déplacement
de S (voir figure n°4). L’aire de la
surface
balayée par le segment (FS) est celle du triangle hachuré sur la figure.
Cette valeur est la demie norme du
produit
vectoriel :
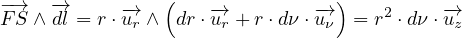 |
(34) |
où 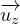 désigne un vecteur perpendiculaire au plan de l’ellipse
orienté vers le lecteur. La nouvelle expression générale de la vitesse
aréolaire est ainsi : :
désigne un vecteur perpendiculaire au plan de l’ellipse
orienté vers le lecteur. La nouvelle expression générale de la vitesse
aréolaire est ainsi : :
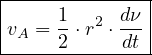 |
(35) |
où 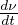 représente le nombre dérivée de l’angle
polaire par rapport au temps, c’est à dire la vitesse angulaire du point
S.
Conclusion : lorsqu’un point S en mouvement elliptique vérifie la
loi des aires, le produit de r2
par la vitesse angulaire est une
constante, souvent notée C et appelée constante des aires :
représente le nombre dérivée de l’angle
polaire par rapport au temps, c’est à dire la vitesse angulaire du point
S.
Conclusion : lorsqu’un point S en mouvement elliptique vérifie la
loi des aires, le produit de r2
par la vitesse angulaire est une
constante, souvent notée C et appelée constante des aires :
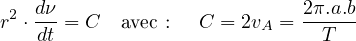 |
(36) |
Nous conservons les hypothèses précisées au début du paragraphe précédent.
Nous reprenons la figure n° 2 en y ajoutant (en bleu) la trajectoire du centre Sf d’un satellite fictif qui décrirait à vitesse constante un cercle de rayon a (demi grand axe réel de l’ellipse), sa période de révolution T étant la période de révolution réelle du centre du satellite. Le centre du cercle est le point F, foyer de la trajectoire réelle elliptique. Le point P représente le périastre. L’angle polaire entre (FX) et (FSf) est noté M. Prenons l’origine des dates à un instant où Sf coupe l’axe (OX). La date t=0 correspond ainsi au passage de Sf et de S au périastre. Si Sf tourne de 2.π radians (360°) pendant la durée T, pendant la durée t, il tourne de :
 |
(37) |
En astronomie, la valeur de l’angle M est appelée « anomalie moyenne » alors que la valeur de l’angle E est appelée « anomalie excentrique ». Le mot « anomalie »désignant un angle peut surprendre. Il provient de l’adjectif « anomal » signifiant : « qui présente des irrégularités ».
À ce stade, connaissant les valeurs du demi grand axe « a » et de l’excentricité « e » de l’ellipse, nous pouvons tracer la trajectoire de S ; nous savons aussi positionner Sf à n’importe quel instant de date « t » sur sa trajectoire circulaire, mais nous ne savons pas encore positionner S sur sa trajectoire elliptique à la date t. Pour ce faire, il faut connaître la position du point Mc puis appliquer la méthode déjà expliquée pour placer le point S. Il faut donc déterminer la valeur de l’angle polaire E à la date quelconque t, ce qui revient à établir une relation entre E et M à un même instant de date t. Pour cela, nous allons appliquer la loi des aires : l’aire balayée par FS entre la date zéro et la date t doit être proportionnelle à t et la durée T correspond à une aire balayée égale à celle délimitée par l’ellipse : π.a.b . L’aire A balayée par (FS), entre les dates zéro et t (coloriée en bleu sur le schéma) doit vérifier la relation :
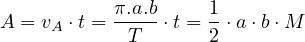 |
(38) |
Exprimons cette aire en fonction de l’anomalie
excentrique E. Exprimons d’abord l’aire A1 du secteur circulaire de rayon a
correspondant à l’arc 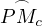 . Lorsque le rayon OMc
tourne d’un tour, soit 2π.
radians, il balaie l’aire totale du disque soit π ⋅ a2
;
lorsqu’il tourne de l’angle E (mesuré en radians), il balaie l’aire
:
. Lorsque le rayon OMc
tourne d’un tour, soit 2π.
radians, il balaie l’aire totale du disque soit π ⋅ a2
;
lorsqu’il tourne de l’angle E (mesuré en radians), il balaie l’aire
:
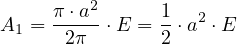 |
(39) |
Exprimons maintenant l’aire A2 du triangle (OFMc). Cette aire est égale au demi produit de la hauteur YMc du triangle par sa base : OF = c = a.e ;
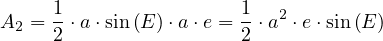 |
(40) |
La différence (A1
- A2)
représente l’aire A3
de la surface délimitée par l’arc  et les segments (FP) et (FMc)
:
et les segments (FP) et (FMc)
:
![1
A3 = A1 - A2 = 2 ⋅a2 ⋅[E - e ⋅sin(E )]](annexe_1_Trajectoire_elliptique81x.png) |
(41) |
Appliquons à tout point du contour dont on vient de calculer l’aire A3 la transformation déjà utilisée : à tout point de ce contour, on fait correspondre un point de même abscisse mais d’ordonnée multipliée par le rapport (b/a) ; l’arc de cercle se transforme en la portion d’ellipse ; le segment (FMc) se transforme en segment (FS) et le segment (FP) se conserve (multiplier l’ordonnée nulle de tout point de (FP) par b/a donne zéro). L’aire A recherchée est donc simplement :
![b 1
A = a ⋅A3 = 2 ⋅a⋅b⋅[E - e⋅sin (E )]](annexe_1_Trajectoire_elliptique82x.png) |
(42) |
Par identification avec l’expression de cette aire obtenue en (33), on obtient la relation recherchée entre M et E démontrée pour la première fois par Kepler :
 |
(43) |
Cette équation n’admet pas de solution explicite littérale. Il faut donc la résoudre numériquement pour une date t donnée à l’aide d’une calculatrice scientifique ou d’un logiciel scientifique (Matlab, Scilab, Maple, programme Python...). Connaissant alors la valeur de E à la date t, on peut déterminer les coordonnées polaires du point S :
* La distance r entre F et S :
![|-------------------|
|r = a⋅[1 - e⋅cos(E)]|--------------------](annexe_1_Trajectoire_elliptique84x.png) |
(44) |
* L’angle polaire ν appelé « anomalie vraie » de S, fournie par les formules (22) ou (27) que je rappelle :
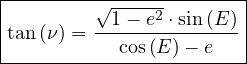 |
(45) |
avec sin du signe de sin
du signe de sin .
.
ou :
 |
(46) |
Les figures ci-dessous représentent les variations en fonction du temps sur une période des trois angles : l’anomalie moyenne M, l’anomalie excentrique E, l’anomalie vraie ν. Pour les faibles excentricités, les écarts entre ces trois valeurs restent faibles ; le mouvement est proche d’un mouvement circulaire uniforme. Le entre O du repère est très proche du foyer F de l’ellipse. Les écarts deviennent important dès que l’excentricité augmente. Conformément à la loi des aires, E et ν ne varient pas à « vitesse » constante. On remarque que, en t=T/2 : M = E = ν = πrad ; quelle que soit la valeur de l’excentricité, si t=0 correspond au passage par le périastre, l’apoastre est atteint à la date t=T/2.
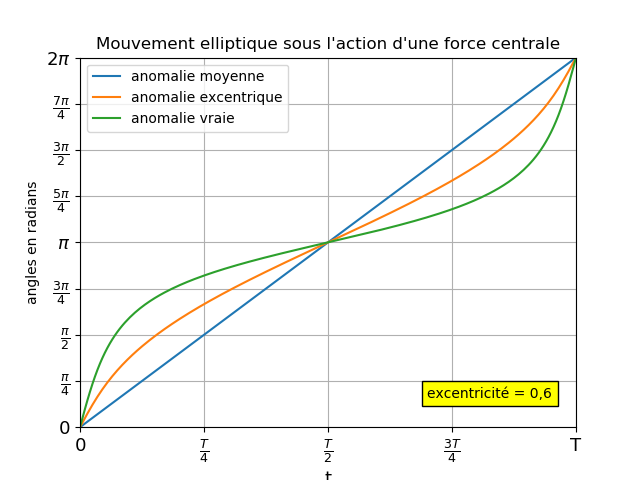
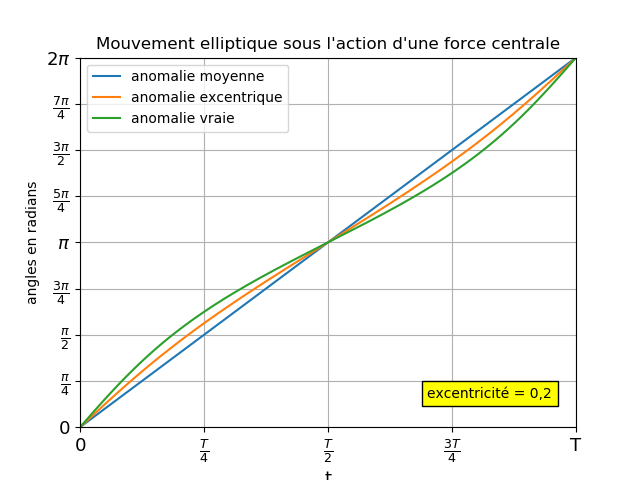
Voici également une animation disponible aux formats mp4 ou avi en cliquant sur un des deux liens ci-dessous ; elle illustre la loi des aires ; On y place quarante positions successives du point mobile sur la trajectoire, prises à intervalles de temps consécutifs égaux ; on remarque bien que la vitesse est plus élevée au voisinage du périastre que de l’apoastre ; de plus, les différents secteurs tracés sont tous d’aires égales :